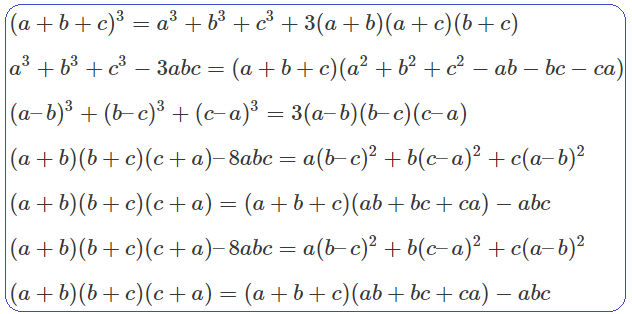Công thức hằng đẳng thức là một trong những khái niệm toán học quan trọng và kỳ diệu. Nó đã và đang chứng minh vai trò và sự ảnh hưởng lớn trong nhiều lĩnh vực khác nhau.
Công thức hằng đẳng thức được sử dụng để biểu diễn mối quan hệ tương đương giữa hai biểu thức. Điều này cho phép chúng ta rút ra các kết luận về tính chất của các đối tượng toán học và áp dụng chúng vào các bài toán cụ thể.
Với công thức này, chúng ta có khả năng giải quyết các bài toán phức tạp một cách nhanh chóng và hiệu quả. Nó giúp ta suy luận, phân tích và giải quyết vấn đề một cách logic và khoa học.
Sự kỳ diệu của công thức này không chỉ xuất hiện trong toán học, mà còn lan rộng vào các lĩnh vực khác như khoa học tự nhiên, kinh tế, xã hội… Công thức này đã góp phần vào việc tiến bộ của con người trong việc hiểu biết và ứng dụng tri thức vào cuộc sống hàng ngày.
Với sự kỳ diệu của công thức hằng đẳng thức, ta có thể khám phá và khai phá những điều mới mẻ, tìm ra những giải pháp sáng tạo và tiến bộ trong nhiều lĩnh vực. Nó là một công cụ mạnh mẽ và không thể thiếu trong việc nghiên cứu và ứng dụng tri thức.
Cách Sử Dụng Công Thức Hằng Đẳng Thức Trong Cuộc Sống Hằng Ngày
Công thức hằng đẳng thức là một công cụ quan trọng trong toán học, nhưng chúng cũng có thể được sử dụng trong cuộc sống hàng ngày. Dưới đây là một số ví dụ:
- Công thức hằng đẳng thức của diện tích hình vuông có thể được sử dụng để tính toán diện tích của một mảnh đất hình vuông.
- Công thức hằng đẳng thức của diện tích hình tròn có thể được sử dụng để tính toán diện tích của một chiếc bánh.
- Công thức hằng đẳng thức của thể tích hình lập phương có thể được sử dụng để tính toán thể tích của một chiếc hộp.
- Công thức hằng đẳng thức của thể tích hình trụ có thể được sử dụng để tính toán thể tích của một chai nước.
- Công thức hằng đẳng thức của diện tích bề mặt hình cầu có thể được sử dụng để tính toán diện tích bề mặt của một quả bóng.
- Công thức hằng đẳng thức của chu vi hình vuông có thể được sử dụng để tính toán chu vi của một tấm thảm.
- Công thức hằng đẳng thức của chu vi hình tròn có thể được sử dụng để tính toán chu vi của một chiếc vòng tay.
- Công thức hằng đẳng thức của chu vi hình lập phương có thể được sử dụng để tính toán chu vi của một chiếc hộp.
- Công thức hằng đẳng thức của chu vi hình trụ có thể được sử dụng để tính toán chu vi của một chai nước.
- Công thức hằng đẳng thức của chu vi hình cầu có thể được sử dụng để tính toán chu vi của một quả bóng.
- Công thức hằng đẳng thức của diện tích hình chữ nhật có thể được sử dụng để tính toán diện tích của một tờ giấy.
- Công thức hằng đẳng thức của thể tích hình chữ nhật có thể được sử dụng để tính toán thể tích của một chiếc hộp.
- Công thức hằng đẳng thức của chu vi hình chữ nhật có thể được sử dụng để tính toán chu vi của một tờ giấy.
- Công thức hằng đẳng thức của diện tích tam giác có thể được sử dụng để tính toán diện tích của một chiếc bánh pizza.
- Công thức hằng đẳng thức của thể tích tam giác có thể được sử dụng để tính toán thể tích của một chiếc cốc nước.
- Công thức hằng đẳng thức của chu vi tam giác có thể được sử dụng để tính toán chu vi của một chiếc bánh pizza.
- Công thức hằng đẳng thức của diện tích hình thang có thể được sử dụng để tính toán diện tích của một chiếc cầu thang.
- Công thức hằng đẳng thức của thể tích hình thang có thể được sử dụng để tính toán thể tích của một chiếc hộp.
- Công thức hằng đẳng thức của chu vi hình thang có thể được sử dụng để tính toán chu vi của một chiếc cầu thang.
- Công thức hằng đẳng thức của diện tích hình tròn có thể được sử dụng để tính toán diện tích của một chiếc đồng hồ.
- Công thức hằng đẳng thức của thể tích hình tròn có thể được sử dụng để tính toán thể tích của một chiếc cốc nước.
- Công thức hằng đẳng thức của chu vi hình tròn có thể được sử dụng để tính toán chu vi của một chiếc đồng hồ.
- Công thức hằng đẳng thức của diện tích hình lập phương có thể được sử dụng để tính toán diện tích của một chiếc hộp.
- Công thức hằng đẳng thức của thể tích hình lập phương có thể được sử dụng để tính toán thể tích của một chiếc hộp.
- Công thức hằng đẳng thức của chu vi hình lập phương có thể được sử dụng để tính toán chu vi của một chiếc hộp.
- Công thức hằng đẳng thức của diện tích hình trụ có thể được sử dụng để tính toán diện tích của một chiếc chai nước.
- Công thức hằng đẳng thức của thể tích hình trụ có thể được sử dụng để tính toán thể tích của một chai nước.
- Công thức hằng đẳng thức của chu vi hình trụ có thể được sử dụng để tính toán chu vi của một chai nước.
- Công thức hằng đẳng thức của diện tích hình cầu có thể được sử dụng để tính toán diện tích của một quả bóng.
- Công thức hằng đẳng thức của thể tích hình cầu có thể được sử dụng để tính toán thể tích của một quả bóng.
- Công thức hằng đẳng thức của chu vi hình cầu có thể được sử dụng để tính toán chu vi của một quả bóng.
- **Công thức hằng đẳng thức của diện tích hình chữ nhật có thể được sử dụng để tính toán diện tích
Bản Dạng Cơ Bản của Công Thức Hằng Đẳng Thức
Công thức hằng đẳng thức (hay còn gọi là phương trình hằng đẳng thức) là một phương trình trong đó hai biểu thức toán học trông giống nhau hoàn toàn. Dưới đây là các bản dạng cơ bản của công thức hằng đẳng thức:
- Công Thức Hằng Đẳng Số:
- Biểu thức bên trái (LHS) bằng biểu thức bên phải (RHS).
- Ví dụ: 2 + 3 = 5, �+�=�+�x+y=y+x.
- Công Thức Hằng Đẳng Phân Số:
- Hai phân số có giá trị bằng nhau.
- Ví dụ: 12+12=121+21=1, ��=��ba=dc nếu ��=��ad=bc.
- Công Thức Hằng Đẳng Trigonometic:
- Các biểu thức trigonometric trông giống nhau.
- Ví dụ: sin2(�)+cos2(�)=1sin2(x)+cos2(x)=1, tan(�)=sin(�)cos(�)tan(x)=cos(x)sin(x).
- Công Thức Hằng Đẳng Đại Số:
- Các biểu thức đại số bằng nhau.
- Ví dụ: �2−�2=(�−�)(�+�)a2−b2=(a−b)(a+b), �3−�3=(�−�)(�2+��+�2)x3−y3=(x−y)(x2+xy+y2).
- Công Thức Hằng Đẳng Hình Học:
- Liên quan đến hình học và các hình học đồng dạng.
- Ví dụ: Tứ giác có tứ giác đồng dạng là tứ giác đối xứng.
Các công thức hằng đẳng thức này là cơ bản và thường được sử dụng rộng rãi trong toán học và các lĩnh vực khác để chứng minh, tính toán, hoặc giải quyết vấn đề.